While working on livestock management software for a client, I got to thinking. How much harder would inbreeding calculations be, if an organism could travel back in time to be its own ancestor? Disclaimer: this has not been peer reviewed, let alone reviewed by anybody with more than a high school level understanding of biology or time travel.
First, let’s start with an incredibly degenerate case. Alice takes her son Bob on a vacation into the future. While then, Bob picks a pretty flower and hides it in his pocket. He names the flower Carol. Upon returning to their native time, Bob immediately runs outside and replants the flower. Some time later, the flower fertilizes itself and produces an offspring, which is later picked up by young Bob.
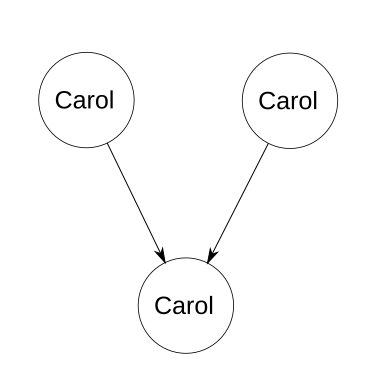
In this case, Carol contributed both of the haploids that merged to form herself. She’s her own parent, twice over. Each of Carol’s homozygous loci has a 100% chance of producing identical alleles in the gametes, and therefore the same homozygous locus in the offspring (which is also Carol). Each of Carol’s heterozygous loci has a 50% chance of giving the same allele to the male gamete as what was in the male gamete that produced Carol; similarly and independently, it has a 50% chance of giving the correct allele to the female gamete. Combined, there’s a 25% chance that a single heterozygous locus will result in the same genetic path that produced itself. However, unlike with normal inbreeding calculations, we know that all the genes of Carol as a child are equal to Carol as the parent. Therefore, let n be the number of loci, and the probability of heterozygosity due to descent is 0.25n. The probability of homozygosity due to descent, i.e., the coefficient of inbreeding, is therefore 1 − 0.25n. Luckily, Alice is a botanist, so when she discovers what Bob did, she teaches her son an interesting lesson about genetics and time travel.

Elsewhere in the world, Dave is a sheep farmer who’s about to go on a business trip to a few years in the past. Unfortunately, things don’t go according to plan, when his prized ewe Eve sees the portable time machine and thinks it’s a bucket of corn. She bumps into Dave, who was already nervous about time travel. He fumbles the time machine, which falls on Eve and activates. Dave spends the rest of the day talking to insurance companies. Meanwhile in the past, Eve meets a very attractive ram named Fred.
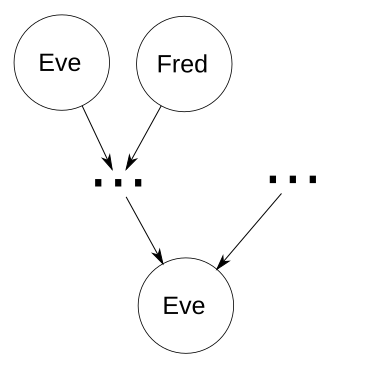
Since this is theory instead of reality, let’s ignore what actually happens next, and instead generalize and assume. Two of Eve’s ancestors are a mated couple, herself and Fred. Without looping, there are n generations from Eve as an ancestor to Eve as a descendant. I.e., n=1 represents Eve as her own parent, n=2 represents Eve as her own grandparent but not her own parent, etc. To make things easier, assume there are no other common ancestors, so that every ancestor of Eve that is not also a descendant of Eve has a coefficient of inbreeding of 0. Tracing genetic paths from Eve0 back n generations gives 2n distinct genetic paths, one of which is to Eve1 herself. Thus, each locus has a probability of 2−n+1 of having an allele passed down from Eve1 to Eve0. For each of those loci, if Eve1 is homozygous at the locus, she’ll pass down the correct allele (the one she got from herself, Eve2). If Eve1 is heterozygous at that locus, there’s a 50% chance she’ll pass down the correct allele. As in the degenerate case, we know that all of the genes that are passed down to herself are the same ones received from herself. So let m be the total number of loci, and the expected number of loci with alleles Eve passes to herself is 2−n+1m. Therefore, the probability of heterozygosity at those loci is 0.5(2−n+1m). The other loci have alleles from unrelated ancestors, so Eve’s total probability of homozygosity is 2−n+1(1 − 0.5(2−n+1m)). Except for small values of n, that’s really not bad at all!
Generalizing these cases into a comprehensive algorithm for calculating inbreeding in the face of time travel is left as an exercise for the reader. But I suspect it involves a multidigraph where each vertex represents an individual organism, and each arrow represents a gamete, pointing from the parent that created the gamete to the child created from the gamete. Then that type of graph can be split into cases, with some subgraphs analyzed separately. I think that would probably give an algorithm that’s a hybrid between the above cases and normal inbreeding calculations, but I’m not sure.
Eli Dupree says
Alright, let me take a crack at this! I’ve taken a college class on evolution and written a book about fictional time travel. ( https://www.elidupree.com/stories/time-travelers-and-how-to-kill-them-a-practical-guide )
Unfortunately, I don’t know any model of time travel where situations like Carol can occur naturally (i.e. without a human writer deciding what happened, which makes discussion of probability meaningless). Not even the “consistent coilers” model that I made to rationalize consistent time travel in general. Sorry! 😛 (I will make up some math later in this post, though.)
Here’s the problem: normally, the idea of probability assumes that causality is acyclic. So the final result is just what happens when you roll each random event in order. With time loops, you can’t do that. So you need a *timeless* notion of the probability that each universe-history (including loops) would occur – you need to determine those probabilities “before time starts”, so to speak. That’s not impossible, but what probabilities would you use? Here are some easy options that don’t actually work:
– “The probability of a history is proportional to the product of the probabilities of all the individual events in it”. This doesn’t even produce a world like our own. The vast majority of worlds are ones where, for each random event, the most likely result happens (almost) every time, and even if you observed some unlikely things happening, you could still expect that you would never see unlikely things again. Same thing for time travel – worlds where time loops exist are much less likely, so even if you observed a time loop, you could expect that no more time loops would happen.
– “All *possible* histories are equally likely (weighted by exact uniqueness)”. This one MIGHT be reasonable, depending on the underlying physics. At least, it might be able to produce a reasonable world where time travel DOESN’T exist. But if loops are possible, then from any starting time, the number of futures that proceed according to regular physics is vastly smaller than the number of possible time travelers that could return to that moment (because time travelers can be ANYTHING, not just things that would arise from straightforward physics). So the world would be a chaos of time loops, everywhere, forever. Subject to any physical limits on the amount of time travel, I guess. If you could somehow make the AMOUNT of time travel correct, stable loops that come from nowhere still have a larger solution space than time travel arising from straightforward human activities, so time loops would basically be a spontaneous physics-event rather than a human thing.
– My “consistent coilers” model, where loops are created by iterative re-running of straightforward physics. This creates a reasonable world (I hope), but never produces Carol because the Carol situation can’t occur on any of the finite iterations.
Now, we COULD make some simplifying assumptions about the exact situation, and get some probabilities. Here goes:
– Carol is the only thing that exists. Nothing else can interfere with the time loop.
– Oversimplifications of genetics are the only physics. Don’t worry about the physics of any other part of Carol.
– All genes have only two alleles, which are equally frequent. There are no mutations.
– All loci in each gamete have independent probabilities of which parent allele goes to the offspring. (Unlimited crossovers with no errors!)
– Given that fixed set of probabilities, what arrangements of alleles have what probabilities of choosing the same arrangement of alleles?
In this model, your math isn’t quite right, especially where you got the counterintuitive result that adding additional independent genes makes the existing genes more likely to be homozygous. Here, let me simplify the math by writing out all of the (independent, equally likely) possible cases for each gene:
AA->AA
AA->AA
AA->AA
AA->AA
AB->AA
AB->AB
AB->BA
AB->BB
BA->AA
BA->AB
BA->BA
BA->BB
BB->BB
BB->BB
BB->BB
BB->BB
After you observe that the output was the same as the input, the remaining possibilities are 8 cases of homozygous and 2 cases of heterozygous, so the coefficient of inbreeding is always 80%, regardless of the number of genes.
So, based on this math, we would assume that Carol will be 80% homozygous. But wait! Inbreeding often causes offspring to be inviable. And another thing we know about Carol is that Carol is viable! In the most extreme case, if we assume that every gene uses strict dominance and the homozygous recessive variant is inviable ( 😛 ), then we can also remove all of the BB cases, so Carol is now 2/3 homozygous dominant, 1/3 heterozygous.
If you need multiple, interacting homozygous recessive genes to get inviability, the math is harder, so I won’t do it. 😛 And anyway, I don’t think this changes the “coefficient of inbreeding” – I think “coefficient of inbreeding” is a simplification that ignores natural selection, so it would still be 80% regardless.
Adding a bit more “realism”, the 80% would probably be the chance that Carol had 2 copies of the same *entire chromosome* (assuming no crossover). And then even if the chromosomes were different, each gene would also have a 50% chance to be homozygous, so you’d end up with 90% homozygous. You could probably add various other forms of “realism”, too, but pretty soon it would break the simplifying assumptions, so that seems like a fool’s errand unless we can come up with a more versatile model for looping time travel.
Anyway, I hope my comments here have been helpful (or at least interesting)!
– Eli
David Mandelberg says
That was a fun read!
I think I was picturing a model where the universe is internally consistent, but external forces can add consistent temporal loops. I.e., probability is a useful tool in the universe, but there are some events with undefined probability because the cause was (is? will be?) not in the universe. So there’s no way to determine the in-universe probability of Carol existing, but given that she does exist, it’s possible to reason about her genetics. I haven’t thought about this model very rigorously though, so maybe it falls apart.
I don’t think it’s safe to assume that alleles are equally frequent. Carol is effectively the only member of her species, so by assuming the alleles are equally frequent, you either have to get 50% homozygous, or contradict the assumption.
Normal inbreeding calculation just lumps every thing other than homozygosity due to common ancestors in the same probability bucket as heterozygosity, which I’m pretty sure avoids needing to make any assumptions about number or frequency of alleles, or about mutations. So something that would be homozygous from descent, but mutates to be heterozygous is still counted as homozygous. And something that would be homozygous due to an allele just happening to be in unrelated ancestors is counted as heterozygous.
That’s a very good point, and one that it seems I conveniently missed in my original analysis. 🙂
Yup, that’s pretty much correct for the non-time-travel case. Coefficient of inbreeding is used to guess at how likely it is that a (sometimes hypothetical) offspring will be viable/healthy/etc., so it’s not useful to include the offspring’s viability as a prior observation in the calculation. With a time loop, I’m not sure whether or not it makes sense to include it as a prior. Side note: the word “prior” amuses me in the context of time travel.
Yes, thank you for the great counter-analysis! It’s good to see that I’m not the only person interested in tackling the important problems in time travel inbreeding calculation. 😉